Desejo a todos um...

Últimas explicações + Matéria para o teste

ÂNGULOS CUJA SOMA É UM ÂNGULO GIRO 

* Estudar no caderno e na página 53



CONSTRUÇÃO DE ÂNGULOS GEOMETRICAMENTE IGUAIS (utilizando a régua e o compasso)

1º Este é o ângulo que queremos construir:

Antes de começarmos a nossa construção precisamos traçar (com o compasso) o arco de circunferência com centro no vértice:

2º E agora a nossa construção:

(este arco foi traçado com a mesma abertura do compasso da 2ª imagem)

(o arco que interseta nesta imagem foi traçado com base na 2ª imagem - e abertura do compasso de um  ponto da semirreta ao  ponto da outra semirreta, em que o arco interseta)

Nota: Alunos esmerei-me para vos deixar uma base de estudo desta matéria... penso que está percetível, tendo como base o que fizemos nas nossas aulas. Qualquer dúvida - pergunta!


SOMA DE DOIS ÂNGULOS

"Para construir um ângulo igual à soma de dois ângulos dados segue os seguintes passos:

1- Traçar arcos de circunferência, no dois ângulos, com a mesma abertura.
2- Traça um dos lados do ângulo, por exemplo GH.
3- Colocar em H o compasso coma abertura igual ao comprimento de BC e traça um arco de circunferência. Encontras um ponto de interseção , ponto I.
4- Coloca em I o compasso com abertura igual ao comprimento de EF e traça um arco de circunferência. Encontras o ponto J.
5- O ângulo HGJ é a soma dos dois anteriores."

(informação retirada de http://ajudaalunos.blogspot.pt/2010/05/angulos-e-triangulos.html)




BISSETRIZ DE UM ÂNGULO:

Aqui podes ver um slide explicativo: (clica no sublinhado amarelo)

 Aprendo a traçar a BISSETRIZ de uma ângulo


E agora, a MATéRIA PARA O TESTE, como prometido:

* Leitura, escrita e representação de frações;

* Frações equivalentes;

* Simplificação de frações. Frações irredutíveis;

* Frações decimais;

* Dízimas;

* Aproximações. Arredondamentos;

* Comparações de números racionais;

* Adição e subtração;

* Propriedades da adição;

* Expressões numéricas;

* Numerais mistos;

* Adição e subtração de numerais mistos;

* Situações problemáticas;

* Reta, Semirreta, Segmento de reta, comprimento de um segmento de reta;

* Posição relativa de retas no plano ( retas concorrentes: retas oblíquas e perpendiculares. retas paralelas: retas estritamente paralelas e retas coincidentes);

* Ângulos e espécies de ângulos (nulo, agudo, reto, obtuso, raso, côncavo e giro);

* Ângulos côncavos e ângulos convexos;

* Pares de ângulos cuja soma é um ângulo giro;

* Soma de ângulos;

* Medição da amplitude de ângulos;

* Construção de ângulos usando o transferidor;

* Construção de ângulos geometricamente iguais, utilizando a régua e o compasso;

* Ângulos adjacentes;

* Construção de ângulos adjacentes usando a régua e o compasso;

* Bissetriz de um ângulo.

E ainda, o MATERIAL:

 * Folha de teste;

 * Régua, transferidor e compasso;

 * Atenção e concentração :)

Dicas de estudo:

para rever:
* Caderno diário;
* ocantinhodaprofteresa;

para praticar:
* Manual até à página 55;
* Livro de atividades até à página 18.

Nota: No início do 2º período, vou precisar de um caderno quadriculado fininho (podem aproveitar para pedir já ao Pai Natal :)) para começarmos a organizar os resumos da matéria. Passem a palavra...

Até breve

---------------------------------------------------------------------------------------------------------------------------

NATACHA  do 5ºG:

Fico contente por saber que continuas a vir ao cantinhodaprofteresa e deixas sempre mensagens tão agradáveis de se ler. Claro que me lembro de ti! ;) Espero que o 8º ano esteja a correr bem :) Um grande beijinho!

ÂNGULOS e mais ângulos...

ÂNGULO
É a região de um plano limitada por duas semirretas com a mesma origem.
Exemplo:

ângulo BOA
vértice - O
lados- semirreta OB e semirreta OA
AÔB = 45º






CLASSIFICAÇÃO DE ÂNGULOS QUANTO À AMPLITUDE:

* Só falta aqui o ângulo nulo ( 0º ), exemplo:

JOGO: ÂNGULOS (é mais difícil do que parece ... está em inglês, pede para apresentá-lo na aula caso não consigas jogar. Para começar clica em "start"; para teres a amplitude do ângulo arrasta o ponto azul que diz "set the angel", para veres se acertaste clica em "check it")



ÂNGULO CÔNCAVO E ÂNGULO CONVEXO

ÂNGULO CÔNCAVO - Mede mais de 180º e menos de 360º

ÂNGULO CONVEXO- Mede mais de 0º e menos de 180º (os ângulos agudo, reto e obtuso são ângulos convexos)

Clica no sublinhado e aprende a construir ângulos, com a explicação interativa:
 Quero.... Construir um ângulo

Pratica:
Constrói, numa folha e utilizando o material geométrico, ângulos com as seguintes amplitudes:
42º, 65º, 90º, 120º, 154º, 170º

Clica no sublinhado e aprende a medir a amplitude de ângulos, com a explicação interativa:
Quero ... aprender a medir a amplitude de ângulos

Pratica:
Imprime a imagem e utilizando o material geométrico descobre a amplitude de cada um dos ângulos:

Exercicio: ângulos para medir

Figuras no plano

RETA, SEMIRRETA e SEGMENTO DE RETA:

Nota um: Onde se lê "recta" deve ler-se reta.
                 Onde se lê "semi-recta" deve ler-se semirreta.

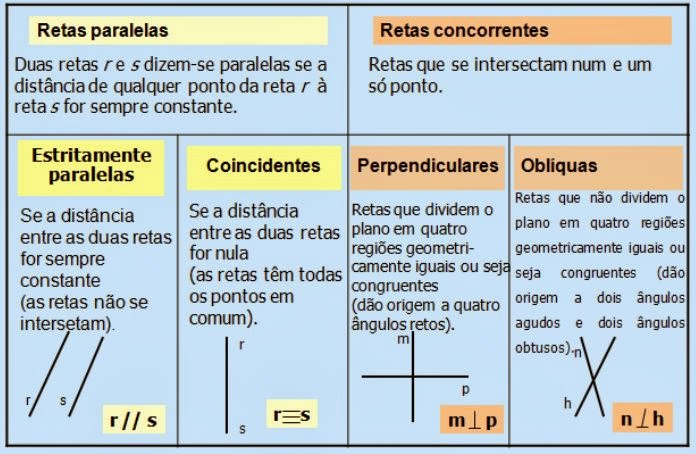
POSIÇÃO RELATIVA DE RETAS NO PLANO:

Para pensares...

1.5. uma reta
        reta BC, por exemplo

1.6. um ponto
      Ponto B, por exemplo

1.7. uma semirreta
       Semirreta AE, por exemplo

1.8. um ângulo reto
        ângulo  EBC, por exemplo

1.9. um ângulo agudo
       ângulo EDB, por exemplo

1.10 um ângulo raso
       ângulo ABE, por exemplo

Adição e subtração de numerais mistos

ADIÇÃO DE NUMERAIS MISTOS:

exemplo:

SUBTRAÇÃO DE NUMERAIS MISTOS: (prestem atenção aos 2 exemplos)

exemplo 1:

exemplo 2:











Cinco exercícios, para treinares a adição e subtração de numerais mistos:

E ainda, mais exercícios... : (clica no sublinhado amarelo)

Clica no link e aparecerão 10 exercícios para resolveres ( a maioria são situações problemáticas :) Precisas de usar papel e lápis, pois não vais lá sem organizares o pensamento e efetuares cálculos. Depois carrega nas mãos que apontam para a palavra resposta e terás a resolução para comparares (não te esqueças que, muitas vezes, há várias maneiras para resolveres o mesmo problema - qualquer dúvida pergunta :))
Exercícios de números racionais





E agora um jogo, para descontrair: (clica no sublinhado amarelo)
Jogo dos Mosquitos - "Operações com frações! Lembra-te de simplificar os resultados e também de utilizares o que aprendeste sobre numerais mistos" Clica no link:
Jogo dos Mosquitos

Mais um jogo de frações (para recordar): (clica no sublinhado amarelo)
Jogo de frações

Bom fim de semana....

Regressarei, em breve, com mais novidades matemáticas fantásticas :)

MEDALHAS & MEDALHÍSSIMAS

MEDALHAS (estas são atribuídas por turma):

TURMA 1:
Leonardo - MEDALHA DE OURO
       César- MEDALHA DE PRATA
    Samuel- MEDALHA DE BRONZE



TURMA 2:
Margarida- MEDALHA DE OURO
        Artur- MEDALHA DE PRATA
     Manuel- MEDALHA DE BRONZE



TURMA 7:
Martim - MEDALHA DE OURO
       Rui- MEDALHA DE PRATA
Rafaela- MEDALHA DE BRONZE


MEDALHÍSSIMAS (estas são atribuídas, no blog, às 3 melhores notas destes 9 alunos):

                               Leonardo (turma 1) - MEDALHÍSSIMA DE OURO
 César (turma 1) & Margarida (turma 2)- MEDALHÍSSIMA DE PRATA
                                  Samuel (turma 1) - MEDALHÍSSIMA DE BRONZE

PARABÉNS A TODOS, continuem  a trabalhar e a conquistar medalhas :)

Numerais mistos e frações impróprias

Agora que estamos cansados de trabalhar expressões numéricas (com tanto treino espero que já estejam bem esclarecidas na vossa cabecinha), estou de regresso com mais novidades :

Numerais mistos
Os números racionais maiores que um podem ser representados por numerais mistos.

Como representar um numeral misto sob a forma de fração. Exemplo:

Exercício:
Seguindo esta explicação, que é a mesma que tens no caderno, representa sob a forma de fração:

E depois deste exercício podes jogar este joguinho:

Jogo: E agora um jogo de numerais mistos. Aqui aconselho a utilização do lápis  e borracha. Colecionem muitas caixas certas.

Jogo I: Numerais mistos

Também aprendemos, a escrever uma fração sob a forma de numeral misto. Exemplo:

(Repara que quatro terços é maior que a unidade).



Exercício:
Seguindo esta explicação, que é a mesma que tens no caderno, representa sob a forma de um numeral misto:

Jogo:
Efetua as adições e escolhe o navio que tenha a resposta arredondada à dezena mais próxima (podes aproveitar para treinar o cálculo mental e evitar usar o lápis)
Jogo II: Arredondamentos

Jogo III: Frações equivalentes
Aqui está o jogo da vaquinha, e vais treinar (para não esquecer) as frações equivalentes. Por favor, não deixes o senhor cair à água muitas vezes (ele agradece :)).

PS. Já sabem... se tiverem dúvidas na resolução dos exercícios perguntem. Quando quiserem jogar, cliquem no sublinhado amarelo. 

Até breve...

Propriedades da adição

Errata: Onde se lê "Os parêntesis indicam qual a operação que seve efetuar primeiro."
Deve ler-se:
Os parêntesis indicam qual a operação que se deve efetuar primeiro.

E agora para treinares uma ficha de trabalho sobre esta matéria:

(para aumentares, clica na imagem).

Adicionar e Subtrair Nºs Racionais

ADICIONAR (OU SUBTRAIR) FRAÇÕES COM DENOMINADORES IGUAIS:

(clica na imagem para aumentar)

ADICIONAR ( OU SUBTRAIR) FRAÇÕES COM DENOMINADORES DIFERENTES:

 Para adicionar (ou subtrair) dois números representados por frações com denominadores diferentes, substituem-se as frações por outras equivalentes, com o  mesmo denominador e só depois se efetua o cálculo. Por exemplo:

Podem consultar uma explicação mais completa neste link:

Adicionar e subtrair frações 

(Já sabem como é, primeiro cliquem no sublinhado amarelo e quando abrir vejam/ explorem as 6 páginas do slide).

E depois desta revisão, estão aptos para resolverem o seguinte trabalho autónomo:

Não se esqueçam de apresentar o resultado na forma irredutível (clica na imagem, para aumentar):

E agora, um jogo para somar e subtrair frações.

 Jogo: PRODIGI

 1º clica no sublinhado amarelo.

2º clica no "Jogar Agora".

3º clica em "Ensine-me" para rever e recordar conteúdos.

4º clica em "Como Jogar" para veres as regras do jogo.

5º clica em "Jogar" e regista as pontuações numa folha sempre que jogares e tenta melhorá-las.
BOAS JOGADAS!


Nota1:  Não resolvam mentalmente. Sugiro que  resolvam numa folha e só depois é que devem colocar o resultado no computador.

Nota2: Poderão surgir operações com numerais mistos - essas só conseguirão resolver no final desta semana.

Comparação de números racionais

Um breve resumo deste último conteúdo trabalhado na aula:

* Frações cujo o numerador é menor que o denominador representam números menores que 1 (Frações próprias). Exemplos:

* Frações em que o numerador e o denominador são iguais representam a unidade. Exemplo:

* Frações cujo o numerador é maior que o denominador representam números maiores que 1 (Frações impróprias). Exemplos:

* Dadas duas frações com o mesmo denominador, representa um número maior a que tiver maior numerador. Exemplo:

* Dadas duas frações com o mesmo numerador, representa um número maior a que tiver menor denominador.



Resumindo:

E depois da explicação, vem uma ficha de trabalho para praticares:
(clica em cima da imagem que aumenta e qualquer dúvida, não exites em perguntar)

E agora é a hora da diversão...

JOGO1:
Um jogo sobre frações (para recordar):

Clica no sublinhado amarelo e prepara-te para ganhar a taça de automobilismo:

Corrida de automobilismo

Instruções:

1. Escolhe a fração que corresponde à parte amarela. Para isso tens de selecionar uma das três frações que te são mostradas.

2. Quando responderes a várias questões corretamente, o carro arranca e ganhas a taça.

3. És capaz de ganhar a taça??? Boa corrida ;)




JOGO2:

Também para recordar, sobre equivalência de frações (clica no sublinhado amarelo):

Jogo do macaco - frações equivalentes

Arrasta o macaco para a argola correspondente à fração equivalente.

Quando completares o nível, clica no retâgulo que diz "Next" pois o jogo continua para um nível de dificuldade maior.

Boa jogada!



Voltarei em breve, com a adição e subtração de números racionais não negativos. Até lá... boa sessão de estudo e um bom divertimento!